Recap: We’re on Zoombini island, full of cute little zoombinis, which are metaphors for group elements. The zoombinis have a magical cloning /merging machine that works like the binary operation for a group and follows the group laws. Last time, we described how we could study a zoombini group and came to some isomorphisms:
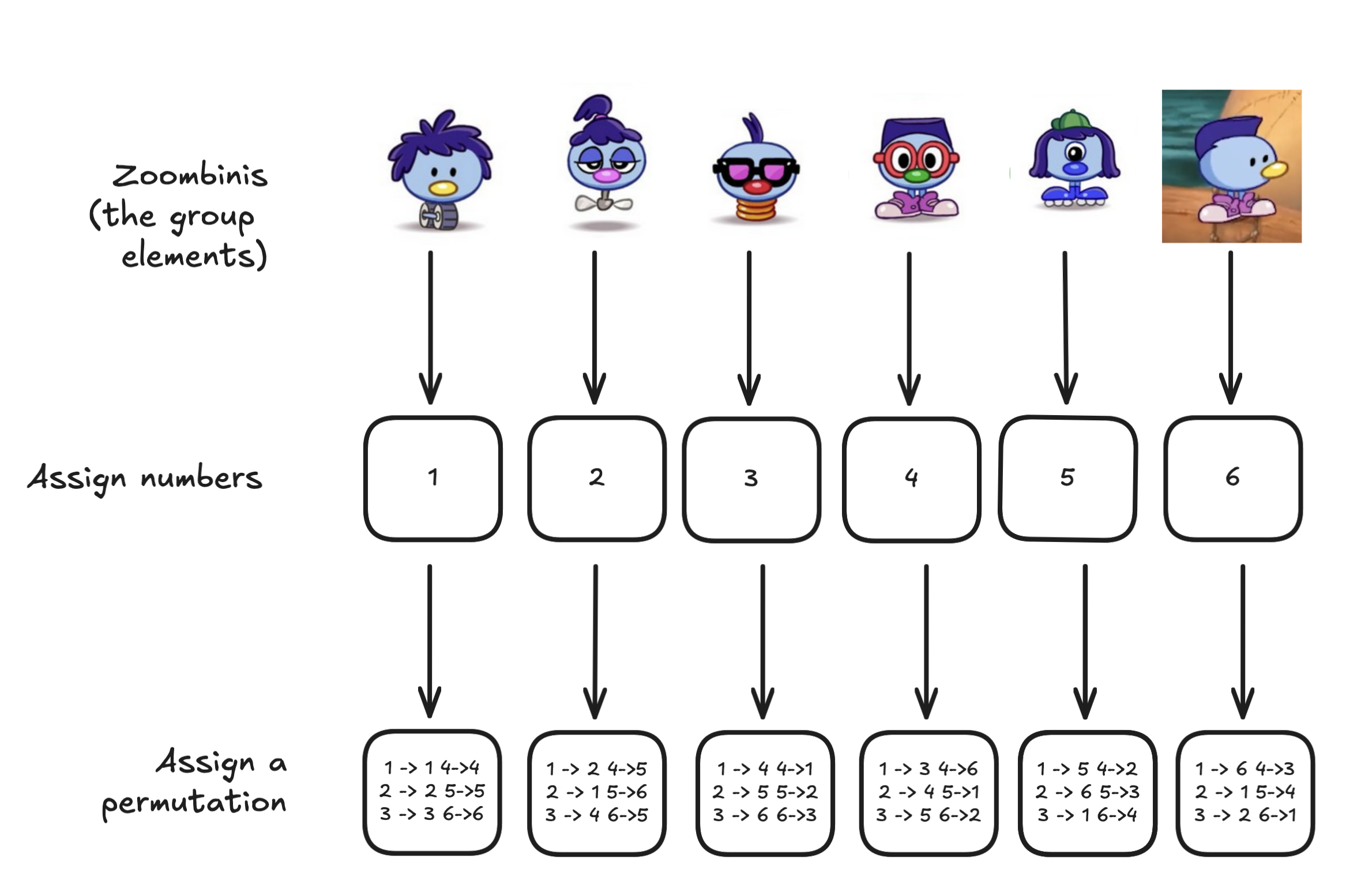
We had started from a group of zoombinis, assigned each zoombini a number, then written a notebook page per zoombini, with the numbers 1 through N in a different order. We had extracted the information about the outcome of the zoombini cloning machine and rewritten it in permutation form, so that we could think of each zoombini as a permutation of the numbers 1->N. This is a “permutation representation”, and it’s so important it’s called the (left) regular representation of the group.
What do zoombinis do in their free time? I’m glad you asked. Their favorite activity is “acting on stuff”. They tell you it’s a mix of “jamming, alchemy, and transmuting”…
They all get up on a stage, but instead of performing a play, they start to pulsate and shake, like exorcists. They start to shake in the same direction, to focus their energy towards where the audience would be sitting, but there’s no audience… In the seats they’ve placed different colored gemstones, one per seat. Ah, they’re acting on the set of gemstones!

Right now they’re warming up on a small set of three gemstones: a red, a blue and a green one. You watch as a blue zoombini walks up to the front of the stage and performs its “action”. The gemstones start to glow, almost magically. Then, poof, the green gemstone turns blue, and the blue one turns green! (The red gemstone doesn’t change).

One by one, the other zoombinis in the group step up and “act” on the three gemstones.
- The small zoombini turns red->green, green->blue, and blue->red.
- The tall zoombini turns red->blue, green->red, and blue->green
- The neutral zoombini, naturally, doesn’t change any stones.
- The yellow zoombini swaps red and blue, and keeps green the same.
- The pink zoombini swaps red and green and keeps blue the same.
- The blue zoombini swaps blue and green and keeps red the same.
This group of 6 zoombinis just transmuted 3 gem stones!
You’ve already noticed a few patterns. For any given zoombini, its “soulmate/inverse” zoombini always does the opposite swaps: if they “act” back-to-back, they cancel each other out.
In fact, for any zoombini pair (a, b), if a acts on the set and then b acts on the set, the outcome is the same as a*b acting on the set, where a*b is the outcome of merging zoombini a with b. The action mirrors the cloning/merging machine’s behavior!
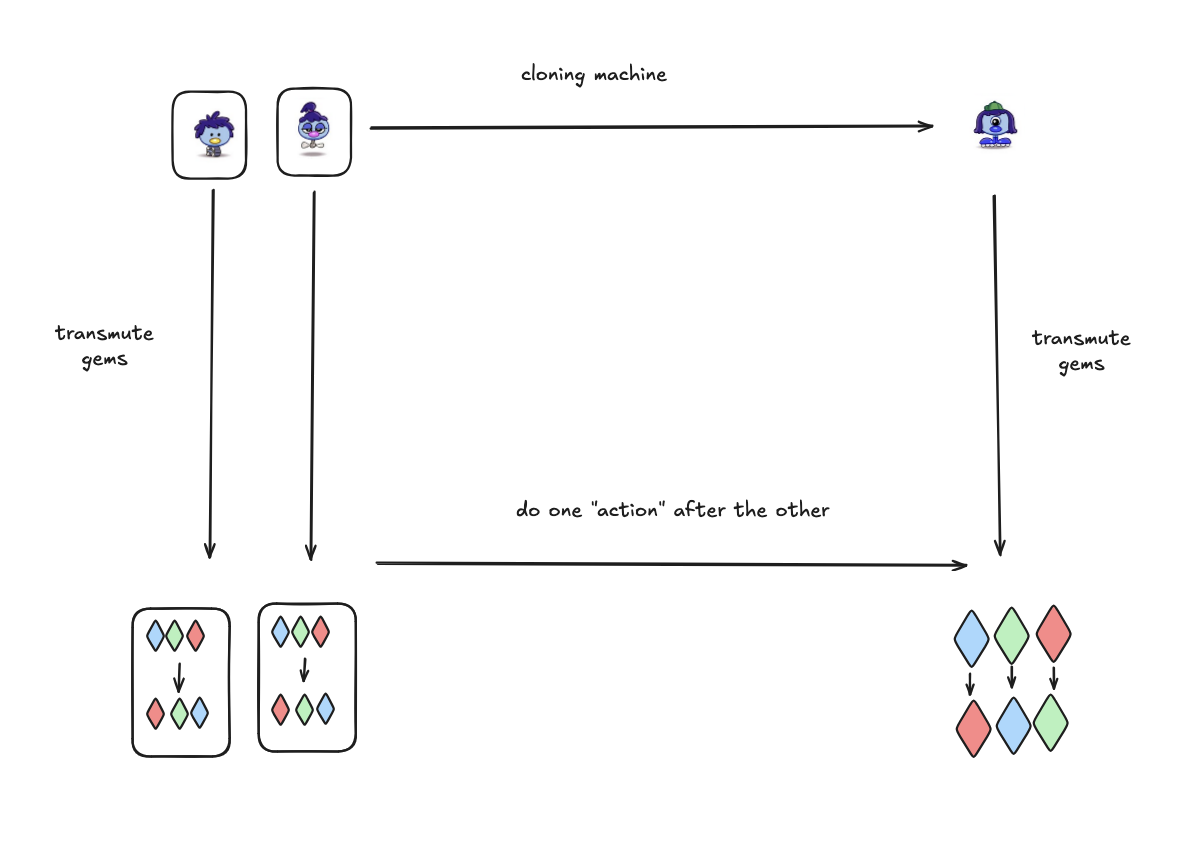
This gives you two ways to predit how an action would play out: You could actually do “small zoombini, then tall, then blue” on the gemstones, or you could merge the zoombinies in the machine first and then have the resulting zoombini act. Inversely, if you wanted to know what result merging (small, tall, blue) zoombinis gives, you could have them act on the gemstones and then look up which zoombini had that exact action.
A Lie Revealed
You’re just watching the last zoombini perform its action, when a big rig of lights and fancy projection equipment falls and crashes on the stage. Wait a minute, they were using this stuff for fancy CGI! They’re not doing magic transmutations! They’re just swapping the gems around when you’re not looking!
Zoombinis have no magical, alchemy-like transmuting powers… We were just fooled by the great stage lighting, and old-school smoke and mirrors. They’ve been each taking a piece of paper and writing down instructions like “swap red<->green, keep blue the same” and passing it to an accomplice behind the scenes, who scurries around underneath the seats and swap the gems. It’s not “transmuting”, it’s just permuting the gems!
Well, though it’s sad to lose the dream that our cute little zoombinis could do magic, we can console ourselves with timeless mathematical wisdom about group theory.
It’s All About Action
You ask all the zoombinis in the group to come to you and hand you the page of instructions they each had written to their accomplish. If you put these all in a notebook, this set of pages containing permutations of gems forms another group!
Let’s write out the mathematical version of our story:
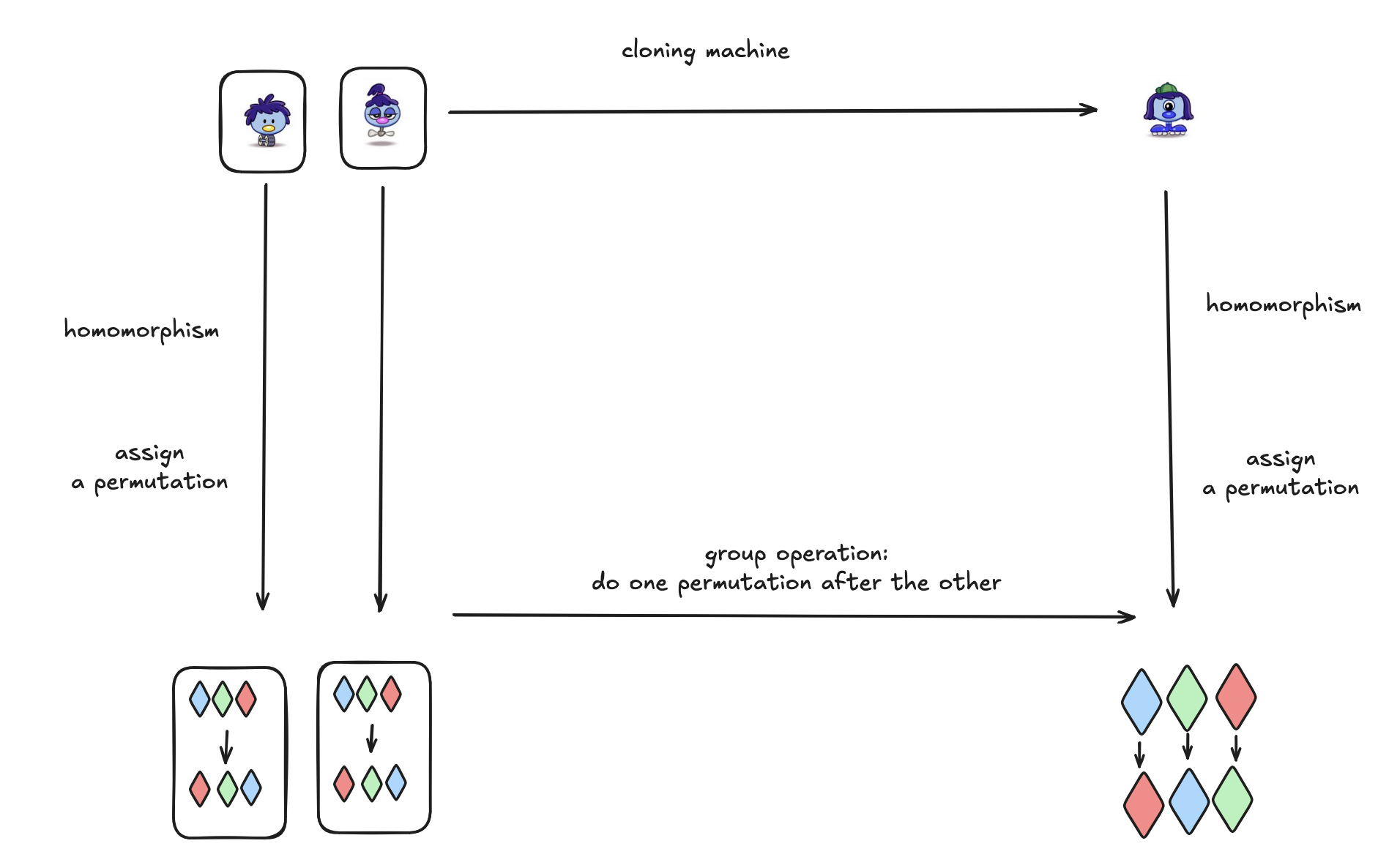
The action of the group G (of zoombinis) on the set S (of gemstones), is a way to assign a member of G (a zoombini) to a function from gemstone -> gemstone , aka a permutation of gemstones. And specifically, these new permutations “combine the same way” as the cloning machine.
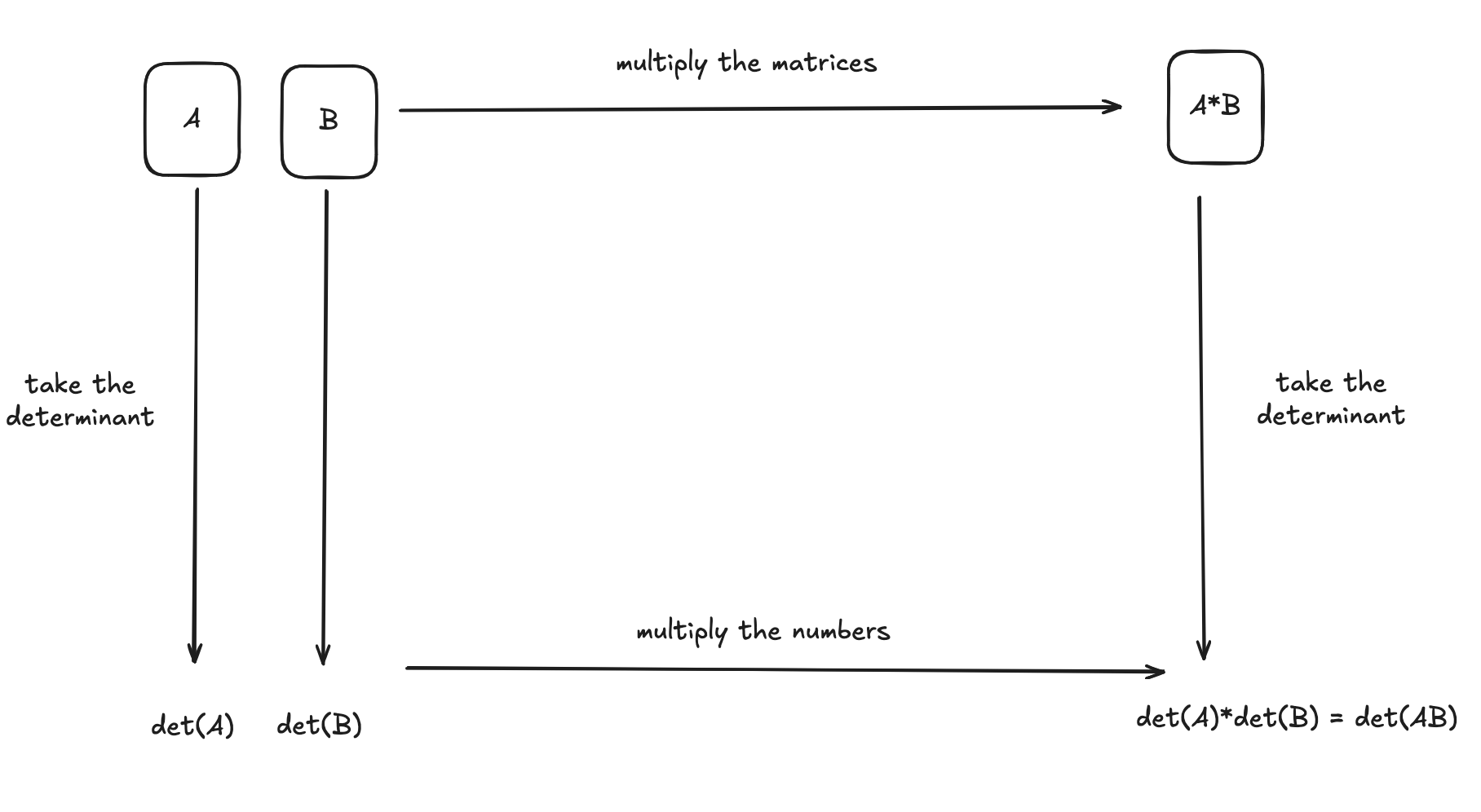
A homomorphism is a transforming function from one group (G) into another (H) G -> H such that transform(a*b) = transform(a)+transform(b), where * is the group operation for G and + is the group operation for H. The result of the transform homomorphism is the same whether you apply the group operation in G or H, so we say it “preserves the group structure”.
As another, more mathematical example, (invertible) matrices are a group where the group operation is matrix multiplication. And the determinant function det(Matrix) -> Real has a a special property that for any two matrices A and B, det(A*B) = det(A)*det(B).
Back to group actions: a group G’s action on a set S is a homomorphism from G to permutations of the set S, where each element of G is assigned a permutation of S. We use “the group of permutations of the set S” so often we gave it a name, it’s “The symmetric group on S”.
This is what it means that a group G’s action on a set S is a homomorphism from G to the symmetric group on S.
Whenever we see a group G, we can think of it as acting on a set S by asking “what homomorphisms can we make from G to the symmetric group of S?”, or we can assume we had such a homomorphism and imagine what properties it would have to have.
Acting different
Zoombinis don’t “act” on just gemstones. They also do sea shells, flowers, fabrics, candies, anything you can put in a set!
A zoombini group can even act in different ways on the same set. Some of the actions can be isomorphic (take the example from above but relabel green and red gemstones), or the actions can be different: Imagine a group of 2 zoombinis acting on a set of 100 sea shells. The neutral zoombini has to do nothing, and the other zoombini has to be its own inverse, so it must swap pairs of sea shells. It can swap any number of pairs of seashells however, so it has many choices for group actions.
Each action is valid, some are just more interesting than others. The most boring action is the one that maps every zoombini/group element to the “do nothing” permutation. It actually satisfies all the requirement for an action, but it’s so uninteresting we call it “the trivial action”.
Staying faithful
You ask the group of 6 zoombinis from earlier (aka S₃) if they can act on two different colored earrings you have in your pocket. They wince a bit, and tell you they don’t like acting on sets this small. In a set with two elements, there are only 2 possible permutations: 1) swap the elements or 2) do nothing. So all 6 of them have to pick between those two options. If the set they act on is too small, there aren’t enough permutations for all of them to have their own action, and multiple zoombinis will end up performing the same permutation. When that happens, you can’t tell zoombinis apart by which permutation they’ve performed and the action is called “unfaithful”.
Unfaithful actions on sets are still valid actions, but they’re not as interesting.
Acting on themselves?
Zoombinis can act on zoombinis? Zomg!
You ask the group of 6 zoombinis to go up on the stage, and then you put a copy of those same zoombinis (doppelzoombinis!) in the seats. You specifically choose for them to sit in the order you wrote down in your permutation representation notebook: zoombini #1 sits in the first seat, #2 in the second seat etc.

When the pink zoombini (#6) walks up and performs the magic, the end result is the exact same as you had written on page 6 in your notebook! It’s as if they took your notebook with the permutation representation and just used it as instructions. Mathematically, the action of “zoombini #6” on the doppelzoombinis is the same result as “put zoombini 6 on the left of the merging machine with the doppelzoombini”

This action is the same as putting the zoombini on the left of the cloning machine.
In algebra terms, the fact that we can put a copy of the group in the seats is stated as: “a group can act on itself via left multiplication”. The action takes a zoombini z from G and assigns it the permutation “zoombini x goes to -> cloning_machine(z,x)”.
I might not sound that interesting, because we haven’t learned anything new. We’ve taken Cayley’s theorem which gives us an isomorphism from G <-> Symm(G), and then applied it as the homomorphism G -> Symm(G) to say G acts on itself.
But it’s a starting point for looking at how G interacts with itself. In general, group actions are a much more interesting way to look at groups than the cloning machine, as we get to apply groups to anything in the wider world and not just other group elements.
Stay tuned for part 3! We’ll see other ways zoombinis act on themselves, as well as orbits and transitive actions.
comments powered by