Inquiries-Week 4: Triangulate the Triangle

Introduction

In this inquiry, triangles are dissected into smaller triangles with vertices labeled as either light (L), medium (M), or dark (D). Any triangles that are LMD triangles are shaded with color.

Triangle play

Let's start with a triangle LMD:

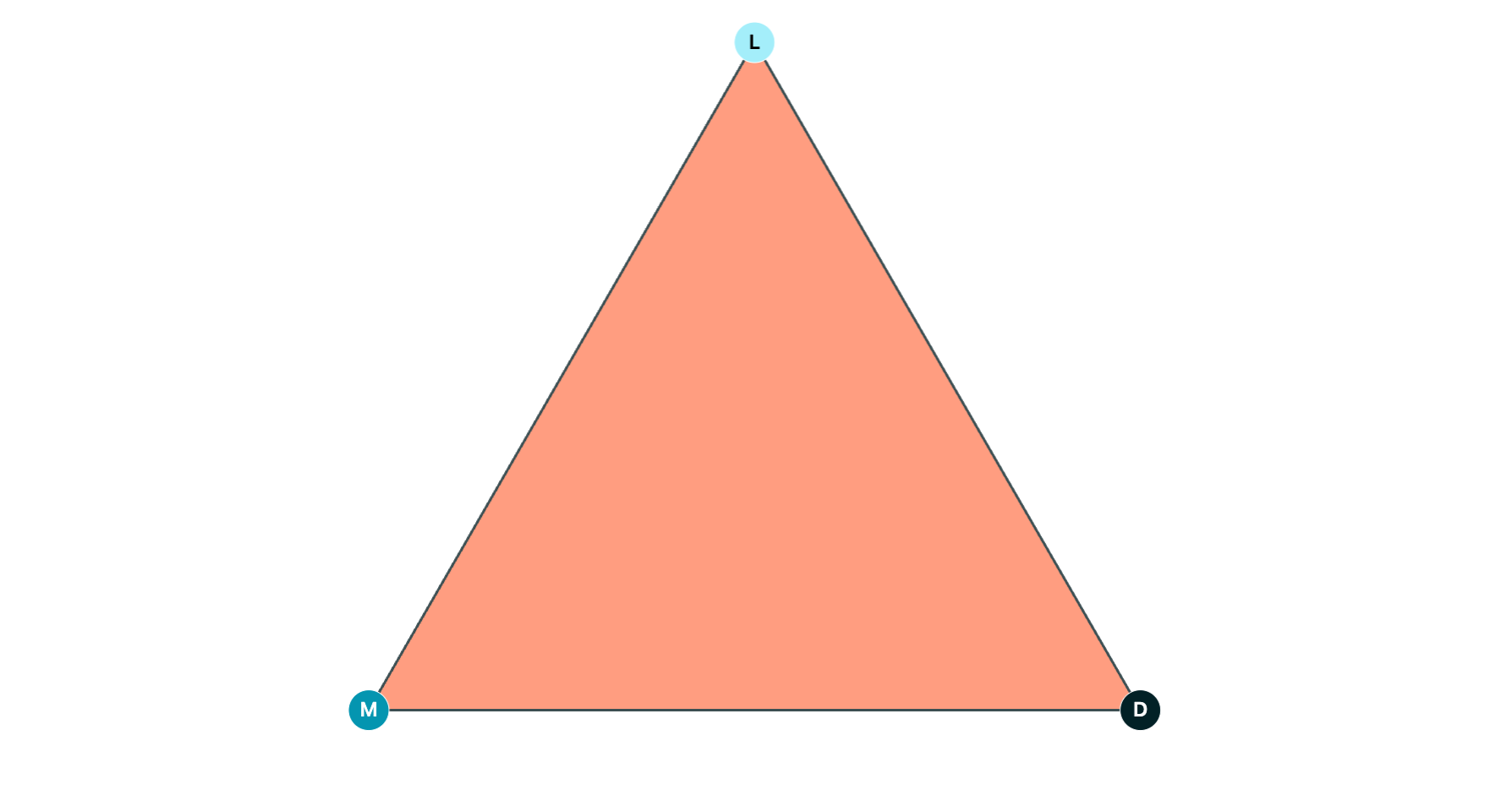
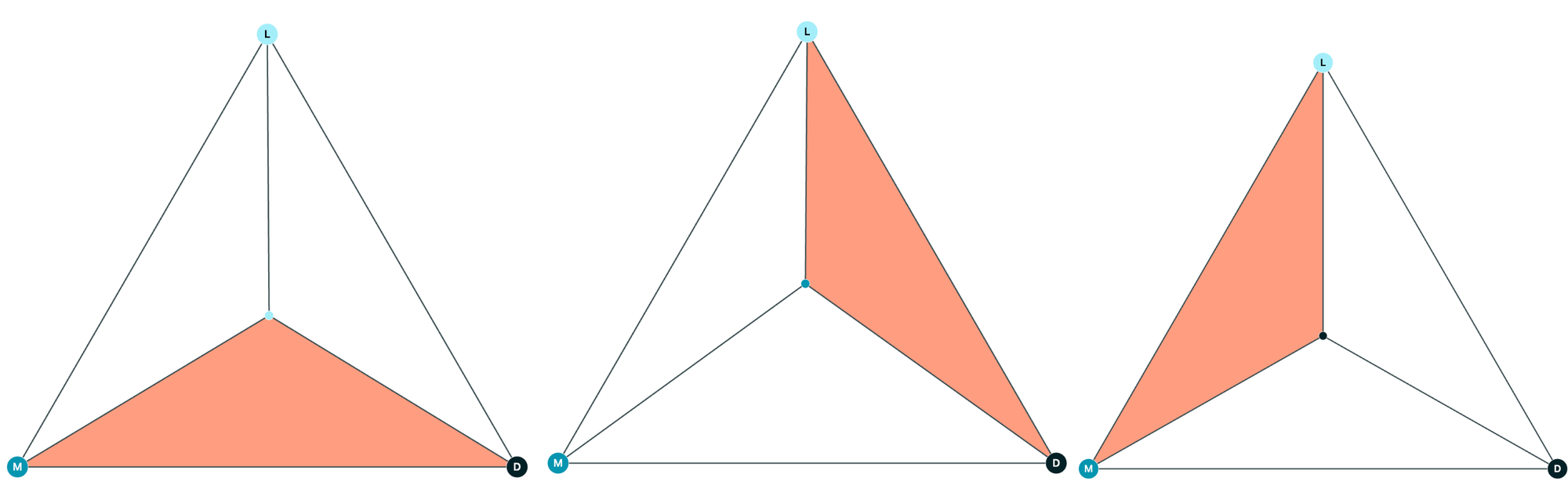
Now, let's dissect the triangle by adding a point somewhere inside and marking it as L, M, or D (for this one, let's use L). And we'll shade in any triangles that have a light, medium, and dark vertex:

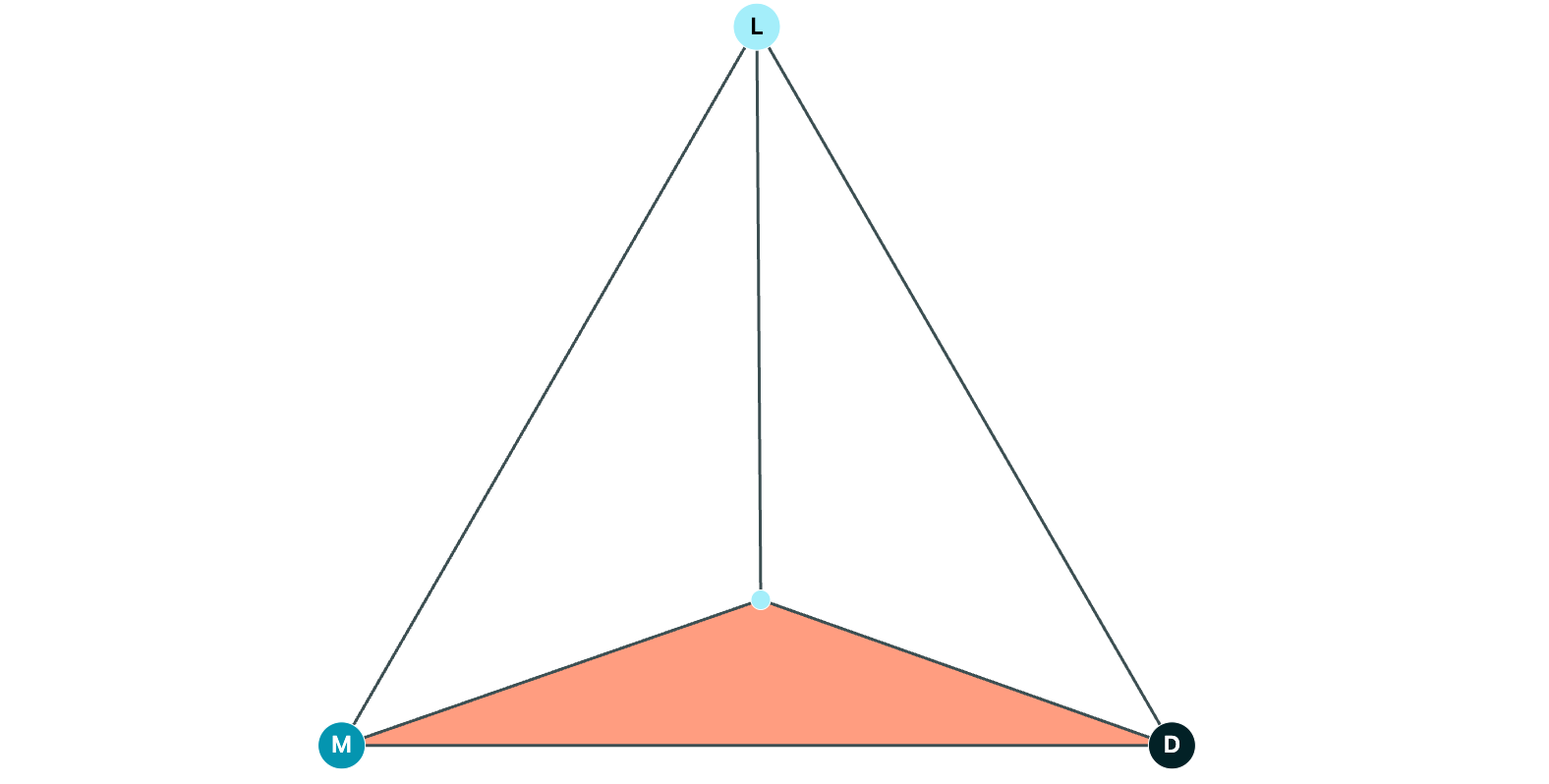
Let's add more L, M, and D points, and connect them to the vertices of their containing triangle. We'll shade the LMD triangles with color:

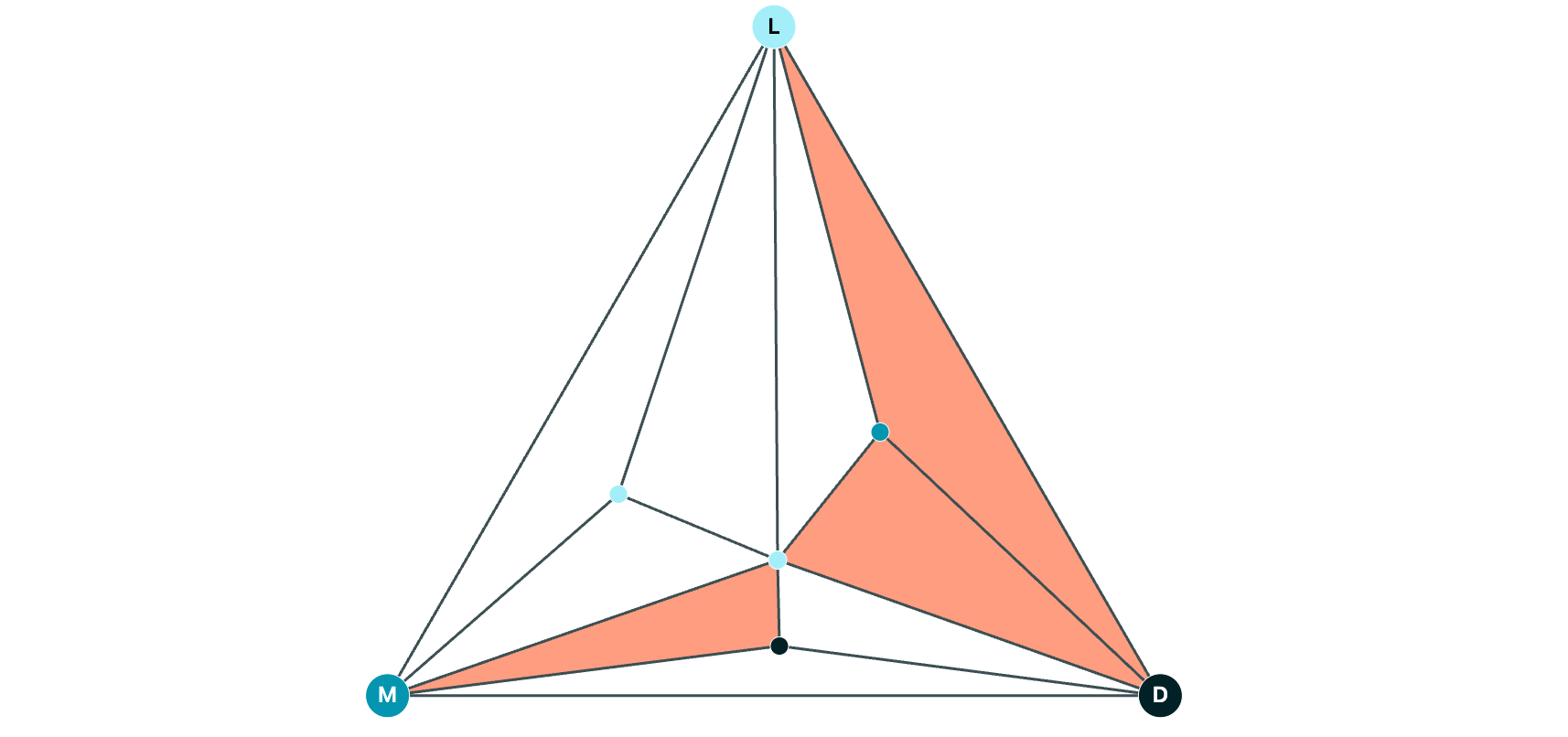
Try it (click on an L, M, or D, then click on the triangle) (full page version is here):

Activity

• Play with adding vertices in lots of different ways.
• What patterns do you notice? What conjectures can you form from your observations and play?
• Is there a minimum number of shaded triangles? A maximum?
• What other questions can you pose?

Proofs (optional)

• How could you approach a proof for one of your conjectures?

This is a 30-60 minute activity.

Exploration Phase 1 (10-15 minutes)

Playing with triangle dissections

Explore adding L, M, and D vertices to triangles and observe which new triangles get shaded. Some of the ways learners may approach this:

• Whiteboard group work (virtual or in person)
• Using the interactive tool and taking screenshots to share
• Drawing by hand on paper (don't color until all vertices are added)
• Creating systematic diagrams showing different vertex placement strategies
• Keeping track of shaded triangle counts with different configurations

Conjecture Formation (5-15 minutes)

Allow for time to write down observations and form conjectures. Give examples of conjectures if needed, that don't give away discoveries.

Possible Conjectures from learners:

"You always have at least one shaded triangle."

"The number of shaded triangles depends on how you place the new vertices."

"When adding a vertex to an unshaded region, there are either zero or two triangles added that are shaded."

"You can't add more than two shaded triangles at a time."

"There is always an odd number of shaded triangles."

Discussion (10-20 minutes)

Share conjectures, observations, and counting strategies.

Discuss different approaches to vertex placement and their effects on the number of shaded triangles. What patterns emerged? Which placements seemed to maximize or minimize shaded regions?

If learners haven't explored systematic approaches, guide them toward:

• What happens when you add vertices of the same type?
• Are there placement strategies that guarantee certain outcomes?
• What do you notice about the number of LMD (shaded triangles)?

Optional - Proof Scaffolding

Below are example proof approaches for some of the possible conjectures. These are optional and intended to be conversational, interactive, and flexible, allowing for follow-up inquiries.

Proof-1: There is always at least one shaded triangle.

• We start with triangle LMD, which is shaded by definition.

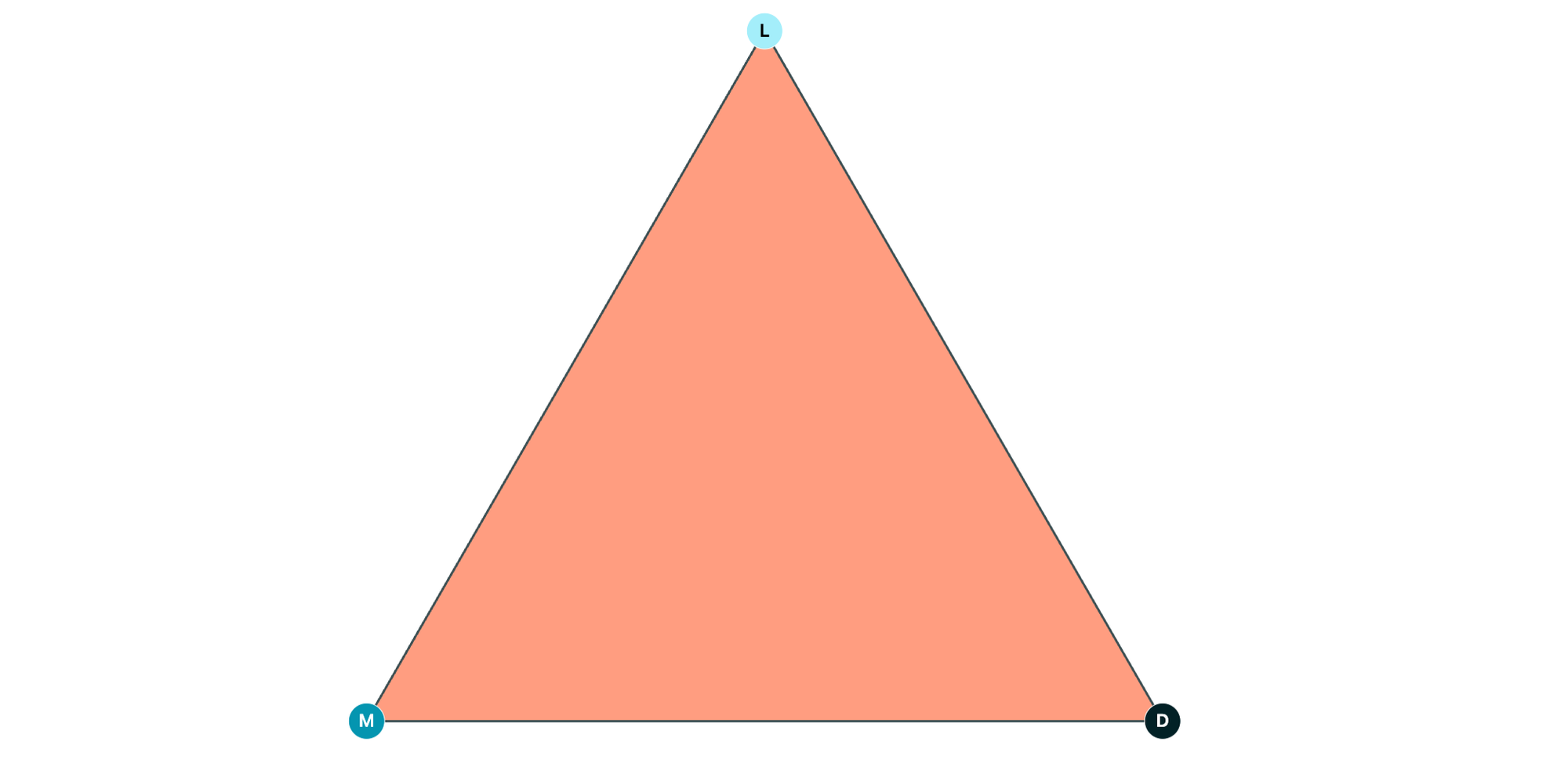
• When we add a new vertex inside the original triangle, we connect it to all three vertices, L, M, and D.
• This creates three new triangles that share the new vertex:
  • One triangle contains the new vertex, L, and M
  • One triangle contains the new vertex, M, and D
  • One triangle contains the new vertex, L, and D
• If the new vertex is L, then the triangles are LLM, LMD, and LLD.
• If the new vertex is M, then the triangles are MLM, MMD, and MLD.
• If the new vertex is D, then the triangles are DLM, DMD, and DLD.
• So, for a new vertex labeled L, M, or D, exactly one triangle will have all three labels L, M, and D and therefore be shaded.

• So, exactly one of the three new triangles will be shaded when a vertex is added in a shaded triangle.
• Therefore, the number of shaded triangles cannot be reduced, and we always have at least one shaded triangle since we start with one.

Proof-2: The total number of shaded triangles is always odd.

• We start with one shaded triangle (which is odd).
• When we add a vertex, we can add it either to a shaded triangle or an unshaded triangle.
• Adding to a shaded triangle: By Proof 1, when a vertex is added in a shaded triangle, the number of shaded triangles remains the same.
• Adding to an unshaded triangle: An unshaded triangle either has two or three of the same vertices (LLL, MMM, DDD, LLM, LLD, MML, MMD, DDL, or DDM).
  • If a vertex is added to a triangle with three of the same vertices, then zero shaded triangles are added, because any new triangle can only have two types of vertices.
  • If a vertex is added to a triangle with two of the same vertices, and the new vertex is one of the two existing vertices, then no shaded triangles are added, because any new triangle can only have two types of vertices.
  • If a vertex is added to a triangle with two of the same vertices, and the new vertex is not one of the two existing vertices, then two shaded triangles are added.
    • LLM becomes: DLL, DLM, DML when vertex D is added. (2 shaded triangles)
    • LLD becomes: MLL, MLD, MDL when vertex M is added. (2 shaded triangles)
    • MML becomes: DMM, DML, DLM when vertex D is added. (2 shaded triangles)
    • MMD becomes: LMM, LMD, LDM when vertex L is added. (2 shaded triangles)
    • DDL becomes: MDD, MDL, MLD when vertex M is added. (2 shaded triangles)
    • DDM becomes: LDD, LDM, LMD when vertex L is added. (2 shaded triangles)
• So, when a vertex is added to an unshaded triangle, either two (even) or zero shaded triangles are added.
• Since we start with 1 (odd), and adding new vertices either adds zero or two, then the number of shaded triangles will always be odd, where:
  • odd + 0 = odd
  • odd + 2 = odd

Tools and Supplies

• Paper, pencils, or a whiteboard.

Vocabulary

• Conjecture: A mathematical statement that is believed to be true but has not yet been proven.
• Dissection: Dividing a triangle into smaller triangles by adding vertices and connecting them.
• Vertex: A corner point of a triangle, labeled in this activity as L (light), M (medium), or D (dark).
• Subdivision: The process of breaking a larger triangle into smaller triangles by adding internal vertices.
• Configuration: A specific arrangement of vertices and the resulting pattern of shaded and unshaded triangles.
• Triangulation: A way of dividing a polygon into triangles by drawing non-intersecting line segments between vertices.
• Parity: Whether a number is odd or even; useful for understanding why certain counts remain odd or even.
• Invariant: A property or characteristic that stays the same even as other aspects of a system change.
• Combinatorial proof: A type of proof that uses counting arguments and systematic case analysis.
• Combinations: The different ways to arrange or select objects, like the different ways to label vertices L, M, and D.

Resources, Extensions, and What Ifs

• Play with this toy to form new conjectures for a triangle filled in with a triangle grid.
• What happens if you start with a different triangle, like LLL or LMM? What patterns hold?
• Higher dimensions: What about tetrahedra with four vertex types (L, M, D, X), where you shade when all four types are present?
• Different Polygons: What if you start with other polygons (like pentagons or hexagons) and use the same triangulation rules with LMD?
• Handshake proof approach