Overengineered Anchor Links

Anchor links are deceptively simple at first glance: click a button, scroll to the heading, and done. But if you ever had to implement them, you might have encountered the . The issue being that, headings towards the bottom of the page can be too far down to scroll them to the desired position. The example component above shows how the ‘conclusion’ heading can never be reached. Surely this will be detrimental to the user experience. We need to come up with a solution. In this blog post, I’ll show some of the solutions I’ve come up with — from a hotfix all the way to unhinged. But before we do that, let’s create a more . Here, we see a viewport moving down the page, with the trigger line being set at 25vh from the top of the viewport. This is what we’ll use to visualize the different solutions.

The most simple solution is to add We calculate the height of the padding by taking the delta between the last heading and the lowest point the anchor trigger can reach. Perfect, right? Well, sometimes the design team is not so fond of random extra padding, so lets keep searching.

Practical: shift the trigger line

Maybe instead of adding extra padding, This is also quite simple to do, we just need to calculate how far from the bottom the last heading is, and put the trigger line there as well. But, this would mean that when the users clicks an anchor tag, the heading could be put all the way at the bottom of the viewport. This is of course not great, since most people put the text they read on the top half of the screen. We need to keep looking.

Good: translate the trigger points

Instead of shifting the trigger line, we could the headings upwards. Instead of using the actual location of the headings as the ones causing the triggers, we create virtual headings and translate them upwards. A virtual heading is not actually visible in the article, its just the position we use to dictate the active state. One might argue that this is pretty much the same as shifting the trigger line, and they’d be right conceptually. However, thinking about translating the trigger points gives us more mental flexibility, as it allows us to consider applying different adjustments based on each heading’s position, which will be crucial later.

The example visualizations now show the location of these ‘virtual headings’. So, while the heading is still at the same place in the article, we visualize where its trigger point is.

In the example, we see one problem arising: the first heading is now too far up. The nice part of this new approach is that we can fix this quite elegantly, since we can shift the individual virtual headings with ease. But what would be a good way to do this?

Great: translate trigger points fractionally

If we think about it, we don’t need to translate all the trigger points. There’s only a few conditions that need to be met:

1. The headings need to be reachable.
2. The headings need to stay in order.

We can meet these conditions by translating the trigger points Here, the first heading doesn’t move, and the last heading moves up by the full amount necessary to become reachable. The other headings move up by a proportional amount based on their position between the first and last heading. Now we are getting somewhere! This is a solid solution. You might want to stop here before your product manager starts giving you puzzled looks, wondering how “fixing anchor links” has suddenly turned into a three-week epic.

Awesome: create a custom mapping function

While the fractional solution works, in the sense that our conditions are met, it does have some flaws. We have chosen a trigger line that’s 25% down from the top of the viewport. It would be nice if we can actually minimize the deviation from this ideal line across all headings. The closer the triggers happen to this (mind you — semi-arbitrarily chosen) line, the better the user experience should be. Minimizing deviation feels like a good heuristic. This for sure will make the users happier and result in increased shareholder value.

Let’s minimize the (MSE) of the delta between the headings’ original positions and their virtual positions. We use MSE because it heavily penalizes large deviations, pushing the system towards a state where most virtual headings are close to their original spots, while still satisfying our reachability constraints. Of course, the constraint that headings must stay in order still applies. This results in all points that are reachable staying at their original position. Seems that we have an issue. headings are bunched up at the bottom. This makes sense, since minimization of the mean squared error only cares about proximity to the original position; it has no ‘force’ that opposes this bunching. We need to define something that encourages the virtual trigger points to maintain a certain distance from each other, ideally related to their original spacing. Considering the user experience, we might assume that it’s nice to have the scroll distance needed to activate the next section’s anchor be somewhat proportional to the actual content length of that section. This ‘sections wanting to preserve their relative scroll length’-force is what we’ll use.

Side quest: minimization functions

To explore this idea we need to bust out… Python. Here, we (read: Claude and I) implemented a solver, which is a type of numerical optimization algorithm designed for constrained problems like ours. The core of the optimization lies in a loss function with two competing terms:

• Anchor penalty: How far a virtual heading is moved from its original location. Minimizing this keeps virtual headings close to their original position. ($L_{anchor} = \sum (y_{virtual} - y_{original})^2$Lanchor​=∑(yvirtual​−yoriginal​)2)
• Section penalty: How much the size of each virtual section (the space between two virtual headings) differs from the original section size. Minimizing this ensures that sections don’t become disproportionately short or long in terms of scroll distance. ($L_{section} = \sum ((y_{i+1, virtual} - y_{i, virtual}) - (y_{i+1, original} - y_{i, original}))^2$Lsection​=∑((yi+1,virtual​−yi,virtual​)−(yi+1,original​−yi,original​))2)

We combine these into a total loss $L = w_{anchor} L_{anchor} + w_{section} L_{section}$L=wanchor​Lanchor​+wsection​Lsection​, where the weights $w_{anchor}$wanchor​ and $w_{section}$wsection​ control the trade-off ($w_{anchor} + w_{section} = 1$wanchor​+wsection​=1).

We define constraints to:

• Keep virtual headings inside the page boundaries.
• Ensure the first heading doesn’t float upward (its virtual position must be >= its original position).
• Keep virtual headings in order ($y_{i+1, virtual} \ge y_{i, virtual}$yi+1,virtual​≥yi,virtual​).

From this, we generate a plot showing how the virtual headings’ locations change as we vary the weights (specifically, as $w_{section}$wsection​ increases from 0 to 1).

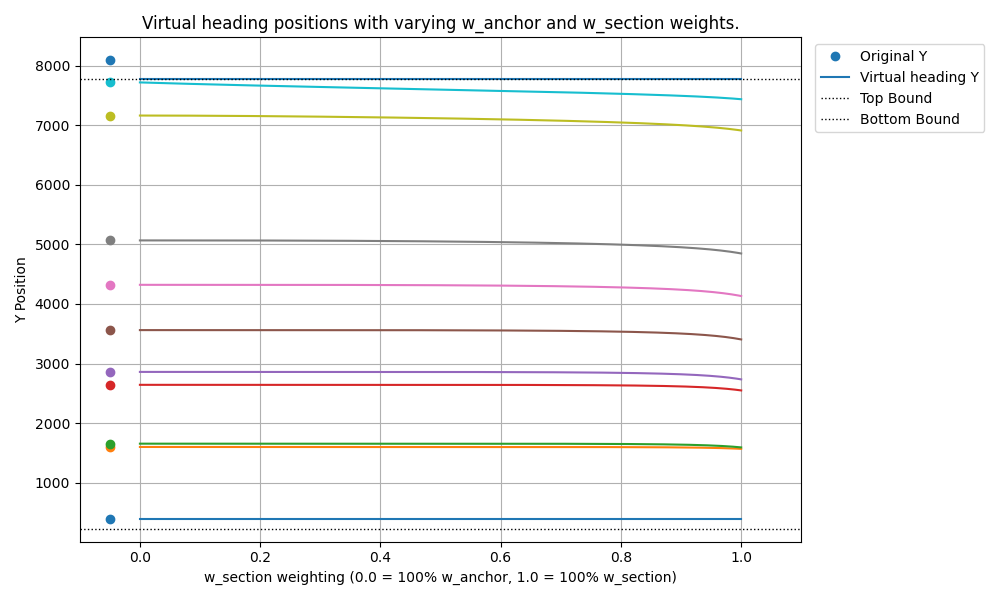
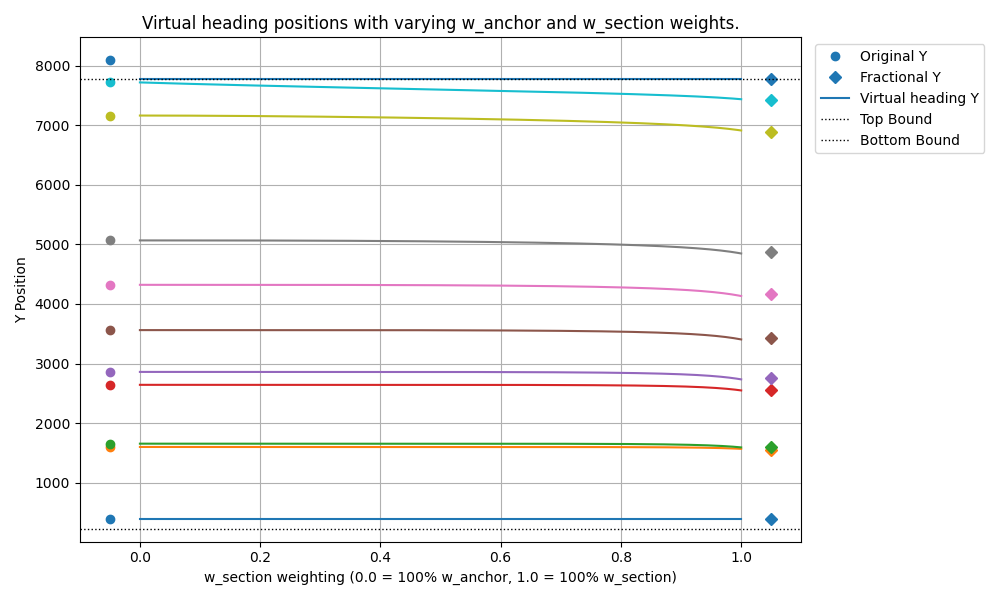
Running that code gives us . The circles on the left (at $w_{section} = 0$wsection​=0) represent the original heading locations. The lines show how each virtual heading’s location (Y-axis) changes as the section penalty weight $w_{section}$wsection​ (X-axis) increases. On the left side, the priority is keeping headings near their original spots (high $w_{anchor}$wanchor​). On the right side, the priority shifts to preserving the original spacing between headings (high $w_{section}$wsection​). I am curious to see how this compares to the simple fractional translation we tried earlier. And wouldn’t , the fractional translation is exactly what the optimizer settles on when the section penalty is dominant ($w_{section} = 1$wsection​=1)!

Realizations

Staring at that optimization graph sparked a thought. Okay, maybe two thoughts. First, that need to preserve section spacing really kicks in towards the end of the page, where headings get forcibly shoved upwards to stay reachable, squashing the final sections together. Second, let’s consider the behavior of the ‘fractional translation’ method on an edge case.

Imagine, if you will, taking the entire Bible, from the “In the beginning” of Genesis to the final “Amen” of Revelation, and rendering it as one continuous, scrollable webpage. (For the tech bros among us: you could alternatively imagine gluing all of Paul Graham’s essays back-to-back). Now, suppose the very last heading, maybe “Revelation Chapter 22”, is just 200 pixels too low to hit our trigger line when scrolled to.

Does our previous ‘fractional translation’ make sense here? It means taking those 200 pixels of required uplift and meticulously spreading that adjustment across every single heading all the way back to the start. The Ten Commandments get a tiny bump, the Psalms slightly more, all culminating in Revelation 22 getting the full 200px boost.

Actually, if you think about it, with a fractional translation, the error (the distance between the virtual and original headings) grows with the page length. So if the page tends to infinity, so does the error! This would of course be sloppy, and something users could immediately notice as feeling off. So how are we going to fix this?

The final version

This leads to our desired behavior for a smarter mapping function:

• For headings near the end of the page, apply more adjustment (act like high $w_{section}$wsection​).
• For headings near the beginning of the page, apply less (or ideally no) adjustment (act like high $w_{anchor}$wanchor​).
• The transition between these states should be smooth.

We need a function that maps a heading’s normalized position $x \in [0, 1]$x∈[0,1] (where $x=0$x=0 is the first heading, $x=1$x=1 is the last) to an ‘adjustment factor’ $y \in [0, 1]$y∈[0,1]. This factor determines how much of the maximum required uplift gets applied to the heading at position $x$x.

We need this mapping function $y = f(x)$y=f(x) to have specific properties:

1. It must start at zero: $f(0) = 0$f(0)=0.
2. It must end at one: $f(1) = 1$f(1)=1.
3. The transition should start gently: $f'(0) = 0$f′(0)=0.
4. The transition should end gently: $f'(1) = 0$f′(1)=0.

It turns out that we can borrow a function from the field of computer graphics to solve this problem. The function is a cubic polynomial that smoothly transitions from 0 to 1 over the range $x \in [0, 1]$x∈[0,1].

$$S(x) = 3x^2 - 2x^3$$S(x)=3x2−2x3

This function provides a smooth transition over the entire range $x \in [0, 1]$x∈[0,1]. But what if we don’t want the transition to start right away? What if we want the adjustment factor $y$y to remain 0 until $x$x reaches a certain point, say $a$a, and then smoothly transition to 1 by the time $x$x reaches 1?

We can achieve this by preprocessing our input $x$x before feeding it into the smoothstep function. Let’s define an intermediate variable $t$t that represents the progress within the transition phase, which occurs between $x=a$x=a and $x=1$x=1. We want $t$t to go from 0 to 1 as $x$x goes from $a$a to 1. The formula for this linear mapping is:

$$t_{raw} = \frac{x - a}{1 - a}$$traw​=1−ax−a​

Now, we need to handle the cases where $x$x is outside the $[a, 1]$[a,1] range.

• If $x < a$x<a, then $t_{raw}$traw​ is negative. We want $t$t to be 0 in this case.
• If $x > 1$x>1, then $t_{raw}$traw​ is greater than 1. We want $t$t to be 1 in this case. (Although $x$x is defined on $[0,1]$[0,1], clamping ensures robustness).

We can achieve this clamping using min and max functions:

$$t = \min(\max(t_{raw}, 0), 1)$$t=min(max(traw​,0),1) $$t = \min\left(\max\left(\frac{x - a}{1 - a}, 0\right), 1\right)$$t=min(max(1−ax−a​,0),1)

This $t$t value now behaves exactly as we need: it’s 0 for $x \le a$x≤a, linearly increases from 0 to 1 for $a \le x \le 1$a≤x≤1, and is 1 for $x \ge 1$x≥1.

Finally, we apply the smoothstep function to this clamped and scaled input $t$t to get our final adjustment factor $y$y:

$$y = S(t) = 3t^2 - 2t^3$$y=S(t)=3t2−2t3

This allows us to use a parameter $a$a (where $0 \le a < 1$0≤a<1) to the normalized position where the smooth upward adjustment of headings begins. Setting $a=0$a=0 gives the original smoothstep over the whole range, while setting $a=0.5$a=0.5, for example, means headings in the first half of the page don’t move at all, and the adjustment smoothly ramps up only in the second half, effectively localizing the change.

Let’s pick $a=0.4$a=0.4 and see what this does. (if you are curious about how I found the 0.4, that might become the topic for a part 2.. Which may or may not involve blind ELO ranking. For updates its easiest to follow me here.)

It’s… .

Validation

So, we are finally done. We’ve gone to depths that no man has ever gone before to fix anchor links. A truly Carmack-esque feat that will be remembered for generations to come. Let’s ask the lead designer what .

… Oh well, at least we got a blog post out of it.

Want overengineered anchor links for your project? Get in touch!